문제
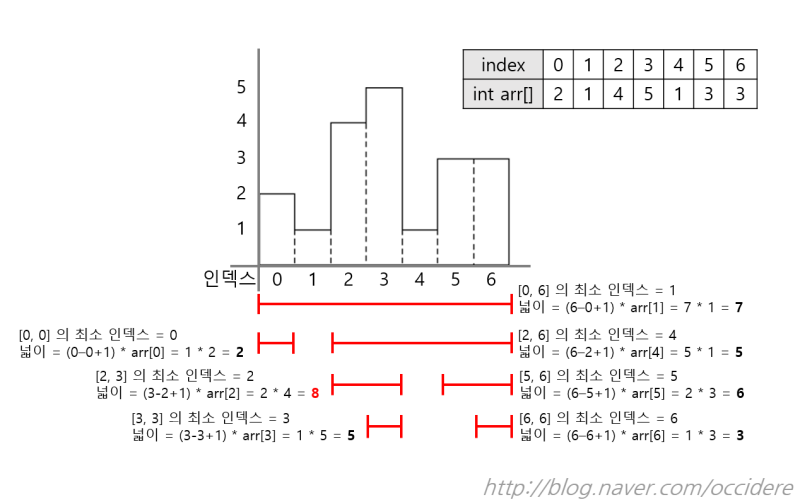
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.

히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
예제 입력 1
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
예제 출력 1
8
4000풀이 방법
첫 줄 ~ N번줄
N: 직사각형의 갯수
N 개의 각 직사각형의 높이
0이 추가되면 종료
0이 될 때까지 라인 입력되면 가장 넓이가 큰 직사각형 넓이 출력
<세그먼트 트리를 이용한 풀이 방법>
세그먼트 트리를 이용하면 nlogn으로 풀어낼 수 있다.
1. 세그먼트 트리를 만들어서 각 노드에 최소 값(최소 높이)의 인덱스를 저장한다.
2. 최대 넓이를 계산하는 query를 호출한다.
가. 제일 처음에는 0 ~ n-1 구간에서 최소 높이가 저장된 인덱스를 찾아낸 뒤, 이를 바탕으로 최소 높이를 산출하고 최소 넓이를 계산한다.
- 위에서 구한 최소 높이 인덱스를 기준으로 삼아서 "왼쪽 탐색", "오른쪽 탐색"의 이진 분할 재귀 탐색을 진행한다.
- 왼쪽, 오른쪽 탐색은 모두 재귀로 이루어지며, 각 탐색은 최종적으로 구할 수 있는 최대 넓이를 반환한다.
- 재귀 호출이 모두 끝나고, 최종적으로 최대값을 비교하여 반환한다.

정답 코드
package test2;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
public class Main {
static int N;
static int inputArr[];
public static void main(String[] args) throws NumberFormatException, IOException {
// TODO Auto-generated method stub
MyScanner scanner = new MyScanner(System.in);
boolean trigger = true;
while (trigger) {
N = scanner.nextInt();
if (N == 0) {
trigger = false;
return;
}
inputArr = new int[N + 1];
for (int i = 1; i <= N; i++) {
inputArr[i] = scanner.nextInt();
}
SegmentTree tree = new SegmentTree(inputArr);
System.out.println(tree.getMax(inputArr, 1, N));
}
scanner.close();
}
static class SegmentTree {
static int tree[];
SegmentTree(int inputArr[]) {
tree = new int[N * 4];
init(inputArr, 1, N, 1);
}
static void init(int[] arr, int left, int right, int node) {
if (left == right) {
tree[node] = left;
} else {
int mid = (left + right) / 2;
init(arr, left, mid, node * 2);
init(arr, mid + 1, right, node * 2 + 1);
if (arr[tree[node * 2]] <= arr[tree[node * 2 + 1]]) {
tree[node] = tree[node * 2];
} else {
tree[node] = tree[node * 2 + 1];
}
}
}
long getMax(int arr[], int left, int right) {
int m = query(arr, 1, N, left, right, 1); // 최솟값 index구하기
// 넓이 계산
long area = (long) (right - left + 1) * (long) arr[m];
// 왼쪽에 막대가 있나??
if (left <= m - 1) {
long temp = getMax(arr, left, m - 1);
if (area < temp)
area = temp;
}
// 오른쪽에 막대가 있나?
if (m + 1 <= right) {
long temp = getMax(arr, m + 1, right);
if (area < temp)
area = temp;
}
// 최대 넓이 반환
return area;
}
static int query(int arr[], int start, int end, int left, int right, int node) {
if (left > end || right < start) {
return -1;
}
if (left <= start && end <= right) {
return tree[node]; // 그 범위를 감싸면 값 반환
}
// 반으로 나눠서 탐색
int mid = (start + end) / 2;
int leftMin = query(arr, start, mid, left, right, node * 2);
int rightMin = query(arr, mid + 1, end, left, right, node * 2 + 1);
if (leftMin == -1)
return rightMin;
else if (rightMin == -1)
return leftMin;
else {
// 둘 중에 더 작은 값은 갖는 index 반환
if (arr[leftMin] <= arr[rightMin])
return leftMin;
else
return rightMin;
}
}
}
static class MyScanner {
final BufferedReader reader;
final BufferedWriter writer;
static StringTokenizer tokenizer = null;
MyScanner(InputStream in) {
reader = new BufferedReader(new InputStreamReader(in));
writer = new BufferedWriter(new OutputStreamWriter(System.out));
}
String nextToken() throws IOException {
if (tokenizer == null || !tokenizer.hasMoreTokens()) {
tokenizer = new StringTokenizer(reader.readLine());
}
return tokenizer.nextToken();
}
int nextInt() throws NumberFormatException, IOException {
return Integer.parseInt(nextToken());
}
long nextLong() throws NumberFormatException, IOException {
return Long.parseLong(nextToken());
}
void close() throws IOException {
reader.close();
writer.close();
}
}
}'Algorithms > 2023 Pro 시험 준비' 카테고리의 다른 글
| 백준 6497 - 전력난 (0) | 2023.07.04 |
|---|---|
| 1647- 도시분할 계획 (0) | 2023.07.04 |
| 구간 합 구하기 백준 2042 (0) | 2023.05.23 |
| 세그먼트 트리 #1 (0) | 2023.05.23 |
| (Normal) React의 생명주기(라이프 사이클) (0) | 2022.09.12 |
